云原生工程师入坑AI深度学习系列(一):从线性回归入门神经网络
Overview
背景
最近团队的业务除了面向通用计算外,越来越多的要处理面向AI场景的软硬件资源的供给、分发、调度等。虽然还是在熟悉的云原生领域,折腾的还是哪些对象哪些事儿,适配到一种新场景。但为了避免新瓶装老酒,能有机会做的更扎实,做出价值,对这个要服务领域内的一些东西也想花点时间和精力稍微了解下。
国庆长假环太湖一圈回来,假期最后这两天豆哥被要求上课,正好难得集中时间可以稍微看些东西。暂时没有精力系统地构建,先入个门。作为一个云原生领域的从业者,目标是知道容器里跑的是什么,怎么跑的。
学新东西时习惯用自己的文字,尽可能简单易懂地总结记录贯通下,做不到严谨、全面、深入、专业。开始前定个小目标只要做到基本的通、透、够用即可。
说干就干,先从深度学习基础技术神经网络开始。Google一把,内容可真叫个多。确实最近身边不管曾经做什么的,摇身一变都能与AI扯上关系。这么多信息对我们这些局外人非常不友好。很多年前自学数学等相关基础课程时,习惯从稍微了解点的东西入手,有点脸熟的东西看着不怵。重拾十来年前尚老师Data Mining那门课程的部分内容,看看老的概念和新的技术能产生哪些联系。
切入点线性回归
线性回归可能是一个比较适当的切入点,模型简单好理解。线性回归时通过一组数据点来拟合线性模型,找出一个或者多个特征变量和目标结果之间的关系,有了这个关系就可以带入条件预测结果。一个非常经典的线性回归例子就是二手房价预测。
影响房价的因素很多,记得当时书上形式化表达是用了一个向量乘法y = wx + b。x向量由(x1,x2,x3,x4)组成,表示若干个属性。这里简单示意下假设只有两个因素x1、x2,分别表示屋子的房间数和面积,也不用向量乘了,就直接写成 y = w1 * x1 + w2 * x2 + b,y就房子价格。其中w1、w2和b称为线性回归模型的参数,w1、w2称为权重weight,b称为偏差bias。
可以看到,作为一种最简单的回归模型,线性回归使用这种线性回归方程对一个或者多个自变量和因变量之间的关系进行建模。有了这个假设的模型,就可以根据已有的二手房成交记录求解出模型上的参数w1、w2和b,这就是老听说的模型训练。完成模型训练求解出线性回归模型的参数,就可以把房间数、面积x1、x2带入表达式,得到房子的预测价格,这就是一个推理过程。
这个一个简单例子把模型的的表达、训练和推理过程最简单地顺一遍。省略了太多的信息和步骤,迭代着加上去应该就是关注的神经网络的关键内容。
首先是模型的表达,通过最基础的数学知识,这个线性回归的输入、输出和运算过程可以大致画成这样。
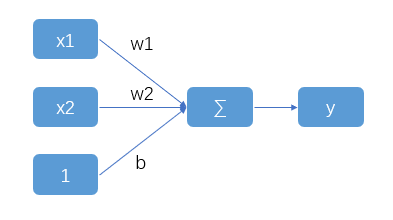
即使完全不了解神经网络,基于最朴素的概念理解,瞅着这个图上这些点的关系好像也已经和神经网络有点神似了。
神经网络的概念
神经网络这个典型术语标准定义很多,总结下简单理解神经网络就是一种模拟人脑处理信息的方式。从数据中获取关联,在输入和输出中建立关系,特别是复杂的输入和输出之间。类似我们人脑中神经元构成一个复杂、高度互联的网络,互相发送电信号处理信息。神经网络由人工神经元组成,在这些神经元上运行算法,求解各种复杂的模型,所以我们说的神经网络完整点描述其实是人工神经网络。
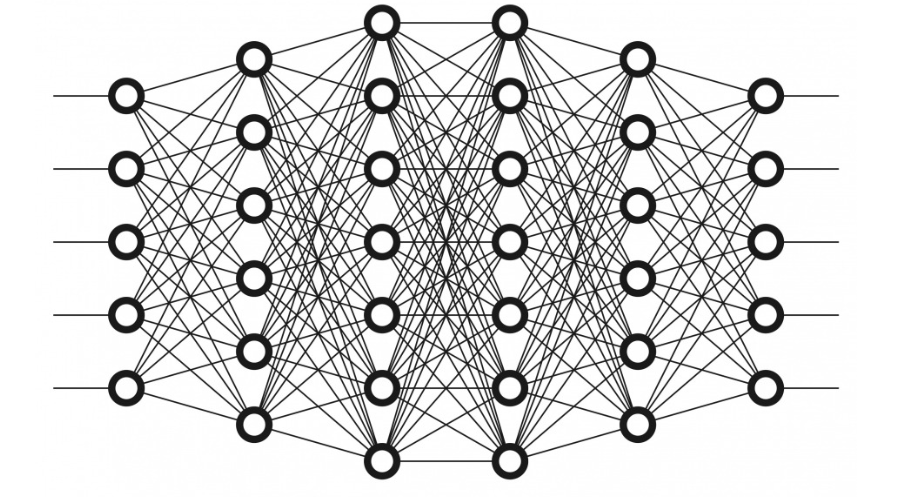
只是从外形简单比较,前面线性回归那个图看上去像一种单层或者单个神经元组成的神经网络,大致可以认为是神经网络的一个简单特例。
神经网络的结构
经典的神经网络包括输入层、输出层和隐藏层。
- **输入层:**接受外部输入的数据,将数据输入给神经网络,简单处理后发给下一层。在预测房价这个线性模型中,输入层就是影响房价的两个属性。在另外一个典型应用图片分类中输入层就是像素,如100*100像素的图片就又10000个输入。
- **隐藏层:**神经网络中大量的隐藏层从上一层,如输入层或者上一个隐藏层获取输入,进行数据处理,然后传递给下一层。神经网络的关键处理都集中在隐藏层,越复杂的模型、表达能力越强的模型,隐藏层的层数越多,隐藏层上的节点也越多。
- **输出层:**输出神经网络对数据的最终处理结果。因为模型固定,输出层的节点数一般也是固定的,如上一个房价预测线性回归的图中,就只有一个输出。如果是分类的模型,一般有几个分类,就对应输出层有几个节点。
不考虑内部复杂实现,只看这个外部结构,从我们程序员的语言看,一个神经网络就像我们编程的一个方法。输入层对应这个方法定义的入参,输出层对应方法定义的返回值,隐藏层可以简单类比我们的方法实现逻辑。模型训练好后,去做推理时就是传入参数调用这个方法,得到返回值的过程。
从数学的视角可能更准确一些,一个神经网络对应一个映射函数,输入层对应函数的自变量x1、x2,输出层对应函数的因变量y。训练过程就是找到函数表达式中的各个参数。有了这个求解的函数表达式,其他任意参数x1、x2带进去也能得到相应基本正确的y。
作为映射函数,只要有一组输入就能映射到一组输出。除了这个根据房子大小、房间数映射出房价外,其他更强大的神经网络可以拟合更复杂的函数。对于大多数深度学习的应用,虽然我们没有办法像这个预测房价的例子这么直观地写出一个具体表达式,但还是可以理解存在这样一个函数映射,或者说通过训练有办法逼近一个理想的函数映射。
记得从哪里看到黄教主说过“AI深度学习,也是一种解决难以指定的问题的算法和一种开发软件的新方法。想象我们有一个任意维度的通用函数逼近器”。如果设计的神经网络足够深、参数足够多,足够复杂就可以逼近任意复杂的函数映射。不只是预测房价这个简单的线性回归,也不只是当年学习的Han Jiawei的Data Mining课本上的分类、聚类、啤酒尿布频繁项这些业务固定的应用。
为了便于理解把以上简单类比总结成下表。
| 神经网络 | 程序视角 | 数学视角 |
|---|---|---|
| 模型 | 代码方法 | 映射函数 |
| 输入层 | 入参定义 | 自变量 |
| 隐藏层 | 方法体实现 | 函数表达式 |
| 输出层 | 返回值定义 | 因变量 |
| 训练 | 构造实现并UT验证修正 | 求解函数参数 |
| 推理 | 实际方法调用 | 带入新的自变量求解因变量 |
| 样板特征 Feature | UT测试用例输入 | 已知的符合表达式的自变量取值 |
| 样板标签 Label | UT用例预期输出 | 已知的符合表达式的因变量取值 |
以上两个临时起意的类别,前一个更像神经网络的物理存在。不管多复杂的神经网络,最终都是一个方法调用。实际应用中通过Restful接口或者其他应用协议调到推理服务上,获得一个输出,返回给调用方使用。而数学的这个类比更像神经网络的逻辑定义,模型本身的定义和模型训练、推理过程。
同时基于这个牵强的类比发现,较之数学和AI模型定义了各种强大、复杂的逻辑表达,我们伟大的程序员才是物理上默默地承担了一切的那个角色。
现在Pytorch、TensorFlow、Mindspore等各种AI框架都很完善了,定义了大量神经网络的层和内置方法,AI算法工程师已经可以直接用Python语言开发算法了。既然AI算法工程师都能写程序来描述算法,我们这些下层做平台、管资源的程序员们也得尝试往上了解一些,起码知道容器里跑的是什么,怎么跑的,怎么用资源,为啥这样用。从而更高效地运行好容器,管好资源,训练出黄老板说的通用函数逼近器,尽管咱现在用的资源不只是他一家的。
有了基本概念,下面还是基于房价预测的例子稍微探究下神经网络中的一些重要过程,首先是神经网络的训练过程。
神经网络训练
前面介绍例子时说过,房价预测模型的训练过程就是将已有的房屋成交记录作为训练集,训练得到线性回归模型。这个求解表达式中参数的过程就可以简单理解为神经网络的训练过程。
详细的理解这个过程前,首先几个简单概念形式化了解下:
- 样板Sample:训练集中每条记录称为一个训练样板Sample。
- 特征Feature:样本的关键属性,即与模型表达有关系的属性。如前面提到的房间数和房子大小,称为样本的特征Feature。
- 标签Label:样本中对应的结果,这个例子中实际成交价格称为标签Label。
基于这个训练集进行模型训练的过程大致是:
- 计算预测结果。将训练数据输入给神经网络,计算预测的结果。这一步就是神经网络中著名前向传播。
- 计算预期结果和训练集中实际结果的差异,并不断调整更新参数,缩小差异,使得模型预测更准确。这一步就是神经网络中最关键的后向传播。
还是基于房价预测例子详细展开下这个过程。
首先,随机分配一组模型参数w1、w2、b的取值作为初始化参数,带入训练集中的样板(x1,x2,y)。注意这个步骤的关键字不是名词”参数“,也不是名词”样本“,而是副词”随机“和形容词”初始化“。神经网络根据输入的x1、x2会求解得到一个预测的房子售价y-predict。通过比较预测房价y-predict和实际房价y的接近程度来判定预测准确程度。对于线性回归一般采用平方函数表示。
第 i 个样本的误差表达是y-predict和y的差平方
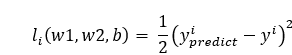
如果全面评估模型的质量,使用训练数据集中所有样本误差的平均值表示:
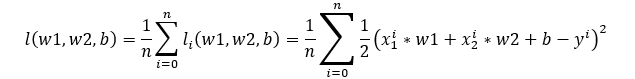
损失函数
不管哪种表达,函数都只跟模型参数w1、w2、b有关系,这个函数称为损失函数Loss Function。模型训练的目标正是求解出参数w1、w2、b,使得损失函数取值尽可能小。把这个损失函数表达的误差画在立体坐标的垂直轴上,参数w和b表达的参数表示在水平轴上则得到如下图。这里只是示意,这个预测房价的例子包含了3个参数w1、w2、b,误差曲面是个空间4维,更一般的多参数是更多维的。
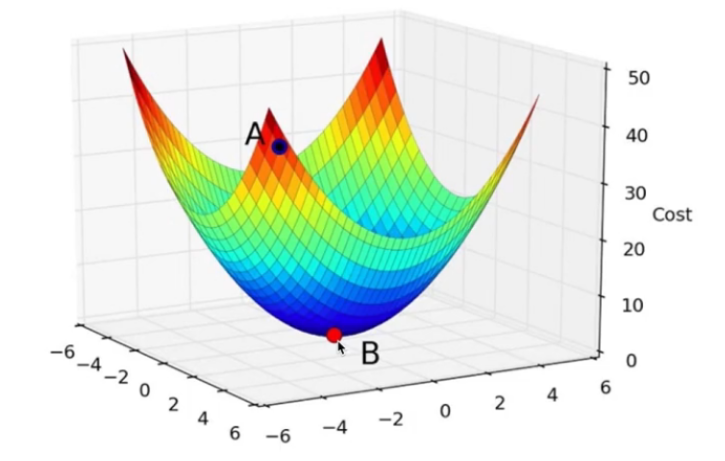
对于这个基于线性回归的房价预测,取得极小值的参数是比较容易算出来。但对于大多数深度学习模型,模型本身比线性回归要复杂得多,并不能直接求解方式得到参数的取值。而需要通过不断迭代的方式使得损失函数获得极小值,这可能就是黄老板说的函数逼近器。试想如果模型参数都能直接求解,训练也就没有那么费劲,当然也不需要那么多资源,黄老板的生意可能也就没有理论支持了。
梯度下降
现在一般应用的是一种叫梯度下降的方法寻找损失函数的极小值。在维基的解释中梯度Gradient是一种关于多元导数的描述。梯度是一个由各个自变量的偏导数所组成的一个向量。平常的一元函数的导数是标量值函数,而多元函数的梯度是向量值函数。
梯度是一个向量,梯度下降法就是函数当前点对应梯度的反方向进行迭代搜索,找一个函数的局部最小值。还是基于房价预测这个例子看,对于(w1,w2,b)组成的这个向量,w1的偏导数的反方向就是在w1这个维度上的变化使得损失函数减小;同样w2的偏导数的反方向就是在w2这个维度上的变化使得损失函数减小。它们的偏导数组成的向量就就决定了一个方向去调整向量(w1,w2,b)的取值,使得损失函数值最小。
基于形式化定义先大致理解到这个程度,幸亏维基在梯度的词条下附了这么生动的解释,帮助我们更好地理解梯度的含义。这样描述的:一个被卡在山上的人正在试图下山,大雾导致能见度非常低,看不见下山的道路。这个人通过观察他当前位置的陡峭程度,找到下山坡度最大的方向前进,从而最快速地下山。坡度 VS 梯度,很形象生动。梯度下降就是利用局部信息找到极小值的路径,即满足损失最小的权重集合。联想到上图的那个损失函数的曲面,山的坡度对应损失函数曲面在这个点的斜率。
粗略总结前面的形式化定义和这个类别,再理解下梯度下降这个动作,梯度指向的在当前点函数值减少最多的方向。而作为一个向量,在神经网络中梯度表示更新权重的方向。
在前面流程描述中,梯度下降使用训练数据集的所有样本数据计算梯度,这种方式也称为批量梯度下降BGD(Batch Gradient Descent) 。很明显一般训练数据量都比较大,这种基于整个数据集计算梯度的方式开销高的基本不能承受。改善方案就是在每次迭代中,随机采样一个样本计算梯度,这就是随机梯度下降SGD(Stochastic Gradient Descent)。实际使用中更多的是随机选择一组样本,使用这一组样本来计算梯度。这组随机样本称为小批量,这种机制就是经常被提到的小批量随机梯度(Mini-batch SGD)。
计算得到梯度后,就可以基于梯度更新参数。这里涉及到一个重要的参数学习率。每次迭代模型参数的变化由梯度和学习率共同作用求得。梯度乘以学习率,得到模型参数在本次迭代后会减少的值。理论上,每次模型参数调整,损失函数取值会减小,模型准确率会提高。
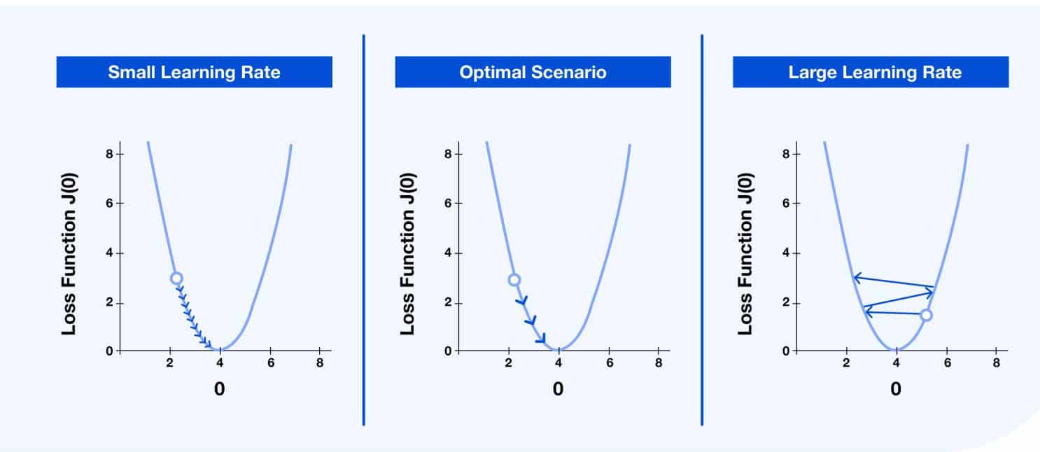
学习率的选择要适当,太小会影响效率,一直不收敛,太大则可能会跳过极值点,错过了最佳值。这个结合下山那个例子也很好理解:下山朝一个方向一次走太多,可能会错过最佳路线,但是一次走太小,没走几步就检查方向也浪费时间。
突然联想到吴军博士《格局》一书中提到的做成事几个关键要素:位置、方向、方法、步伐和节奏。和这里的机制也对应的上,位置对应参数当前取值,方向就是梯度决定的向量更新的方向,步伐节奏可以不严谨地近似对应到学习率。基于当前位置找到前进的方向,并保持一定的节奏前进,终将达到目标点。
除了学习率,小批量随机梯度过程中每次迭代的批量大小batch size是另一个控制训练过程的参数,这类参数称为超参数Hyper Parameter。不同于模型的中的这些参数w1、w2、b都由训练得到,超参数都是预先设定的。一般说的模型调参,调整的就是这些超参数。
说到模型参数,想起在学校里十多年前做过的一个当时号称语义网络的项目Wizag,加州大学的梁教授设计的提取文本Concepts的核心算法被证明非常神奇有用。梁老师作为领域专家指导我们对于这个特定模型进行调参从而获取最优结果。而神经网络中这些需要调整的超参数是模型无关的通用参数。
小批量梯度下降
小批量梯度下降用伪代码描述过程,大致是:
1for i in range (epochs):
2 np.random.shuffle(data)
3 for mini_batch in get_mini_batch(data, batch_size)
4 sum_grad = 0
5 for x1, x2, y in mini_batch:
6 grad = gradient(loss_function x1,x2,y, params)
7 sum_grad + = grad
8 avg_grad = sum_grad / len(data)
9 params = params - learning_rate * avg_grad
基于colab上一个Pytorch线性回归的Notebook,在本地改造为本文中房价预测的例子。在本地环境上简单执行验证,在Python命令行里,逐个片段执行,可以看到不少细节,理解前面的描述的流程。
1import torch
2import numpy as np
3
4inputs = np.array([[]], dtype='float32')
5targets = np.array([[]], dtype='float32')
6inputs = torch.from_numpy(inputs)
7targets = torch.from_numpy(targets)
8
9# 数据集
10from torch.utils.data import TensorDataset
11dataset = TensorDataset(inputs, targets)
12dataset[:3]
13
14# 加载数据集
15from torch.utils.data import DataLoader
16batch_size = 3
17train_loader = DataLoader(dataset, batch_size=batch_size, shuffle=True)
18
19# 初始化模型参数w1、w2和b,随机取一组值
20w1 = torch.randn(2, 3, requires_grad=True) #Weights
21w2 = torch.randn(2, 3, requires_grad=True) #Weights
22b = torch.randn(2, requires_grad=True) # Bias
23
24# 线性回归模型定义
25def model(x1, x2):
26 return x1 @ w1.t() + x2 @ w2.t() + b
27
28# 损失函数定义
29def mse_loss(predictions, targets):
30 difference = predictions - targets
31 return torch.sum(difference * difference) / difference.numel()
32
33# 基于初始化的模型参数,比较预测值与样本集中对应实际值的差异。开始时损失函数取值非常大
34for x1,x2,y in train_loader:
35 preds = model(x1,x2)
36 print("Prediction is :\n",preds)
37 print("\nActual targets is :\n",y)
38 print("\nLoss is: ",mse_loss(preds, y))
39 break
40
41# 50轮epoch后,损失不断减小
42epochs = 50
43for i in range(epochs):
44 for x1,x2,y in train_loader:
45 # 预测值
46 preds = model(x1,x2)
47 # 计算损失,并进行反向传播
48 loss = mse_loss(preds, y)
49 loss.backward()
50 # 基于计算所得的梯度更新模型参数
51 with torch.no_grad():
52 w1 -= w1.grad * 1e-5 # w1 = w1 - w1.grad * 0.00001
53 w2 -= w2.grad * 1e-5 # w2 = w2 - w2.grad * 0.00001
54 b -= b.grad * 1e-5
55 w1.grad.zero_()
56 w2.grad.zero_()
57 b.grad.zero_()
58 print(f"Epoch {i}/{epochs}: Loss: {loss}")
59
60# 训练好的模型对训练集上样本数据x1,x2带入模型,其实就是线性表达式得到对应预测的y,和实际y比较很接近了
61for x1,x2,y in train_loader:
62 preds = model(x1,x2)
63 print("Prediction is :\n",preds)
64 print("\nActual targets is :\n",y)
65 break
正如这个真实的代码实践最后一个片段表达的,模型训练完成后,就可以应用这个训练得到模型进行预测。对应房价预测这个示例就是求解出了参数w1,w2,b即求解出了线性回归表达式,带入x1,x2就可以预测出y。只要知道房子的大小、卧室个数,就能推测出大概能卖多少钱。
过拟合与欠拟合
一般训练好的模型在正式应用前都会有一个机制评价模型预测的准确性。最基本的考察模型在训练数据集上表现出的误差,称为训练误差(Training Error),更实用的是要考察模型在任意一个测试数据结上表现出误差,称为泛化误差(Generalization Error)。
对应的会评价模型是否出现欠拟合Underfitting或过拟合Overfitting的问题。其中欠拟合指模型的训练误差一直太高,即压根儿就没有训练出来。过拟合指模型在测试集上验证的误差远高于在训练数据集上的误差,即训练的挺好,实际验证却不行。
函数复杂度低表达能力弱,不容易找到合理的参数来表达目标模型,容易出现欠拟合。但是太复杂,训练时候能凑出比较好的效果,其实是迎合了测试集的模型特点,适应性弱,在最终测试集上表现并不好,就容易出现过拟合。另外样本数过少也容易发生过拟合。同时保证不出现欠拟合和过拟合对模型设计、训练要求挺高的。个人通俗的理解就是:要平时练习成绩好,同时要最终考试考的好,就要求真正学懂学通。首先要复习到位,即训练样本数量得充分。另外最关键要学懂学通,即掌握了内在的逻辑和模型,而不是只背会了练习的题库,或者只会做题库里的题型不会举一反三,导致练习时候成绩非常好,但是同样的题目换个样到了真正考试又做不出来了。
以上尝试基于一个最基础的线性回归为切入点,描述深度学习的过程。和一个完整的流程比较,以上也只是覆盖了其中关键步骤。
AI基础设施
敲完“关键”两个字,发现有点冒犯同一间办公室里的小伙伴们。我们在这个过程中,完成的模型部署、资源管理、负载调度、模型监控、故障恢复这些不应该轻易说成不关键。特别是现实中当前AI领域卖铲子的重要性,大模型训练最终比拼的还是算力、资源。如何能构建充足的资源满足越来越大的模型训练要求,如何高效地利用好这些稀缺的算力资源,最大化地发挥作用,这是我们发挥作用的舞台。这也就到了我们熟悉的领域了。
在我们支持的客户场景中,找我们要资源的一定不是一个简单的线性回归。如果都是这种简单的模型也无所谓资源管理和调度了,也不需要种卡,在差不多点的单台服务器上就可以运行。很多年前在学校的Machine Learning课上,给尚老师交了个Gini Index的分类训练大作业。当时Java写了数据集加载、模型训练、测试集加载、模型准确度评估,这种简单小程序在当时那个Thinkpad的笔记本上就可以运行。找到我们云厂商提供资源的都是运行大模型或者超大模型的应用场景,模型结构复杂,参数巨大。训练这种模型的算力和内存开销是单机资源无法满足的,单个卡或者现在大多数8个卡组成的服务器也无法存储模型数据或者训练的中间结果。
最具扩展性的方式自然是引入并行训练,把训练任务进行拆分,在多个设备上并行地运行任务,也就是分而治之的思路。不同于之前网格布道的背景经常说到微服务的分而治之把大的单体服务基于业务进行解耦拆分,只是为了开发、测试、部署、运维便捷轻量,是技术上的一种重构,本身从资源层面可以不用拆,大单体也是很好的实践。模型训练的拆分却是不得不拆,简单理解场景更像之前Hadoop为代表的大数据的那种风格。操作对象都是大的数据集,通过分布式方式解决单机的资源瓶颈,并通过并行提高总体的计算效率。
数据并行
模型训练的并行有多种,和Hadoop类似的对数据集进行拆分的是数据并行。类似Hadoop的MapReduce在所有任务执行节点TaskTracker上运行相同的Mapper程序,对分配到该任务节点上的数据切片执行Map操作。模型训练的数据并行一般会把训练数据集在多个GPU上拆分,每个GPU上维护完整的模型和参数。和TaskTracker上每个Mapper对分配的数据集独立的进行Map运算类似,数据并行中每个GPU独立地执行前向传播计算预测值,独立地执行后向传播计算梯度并形成本地局部梯度。同时类似Hadoop的Reduce操作聚合数据,在数据并行中也有一个步骤需要将不同设备上的梯度进行聚合,聚合后的梯度向所有GPU广播并更新参数,这个聚合操作一般通过集合通讯AllReduce实现,连术语名字都和Hadoop的Reduce相似。两者的Reduce操作逻辑上都是在一种特殊的Worker上执行,物理上参与Reduce操作的是多个计算节点。Hadoop的MapReduce会选择多个运行Reducer的工作节点,而模型训练数据并行的AllReduce操作全部GPU节点都会参与梯度聚合,充分利用了每个GPU设备的带宽和算力。
上面这段不严谨的比较,列个表格对照下。
| 比较观点 | 深度学习数据并行 | Hadoop MapReduce |
|---|---|---|
| 并行方式 | 数据切分,计算复制 | 数据切分,计算复制 |
| 分布式计算节点形态 | 每个卡设备 | 每个TaskTracker任务节点 |
| 计算复制方式 | 每个卡维护完整的模型和参数 | 每个TaskTracker上分发相同的Mapper的Jar,执行相同的Map操作 |
| 数据切片 | 小批量样本 | 切分的Input数据 |
| 数据集存在形式 | 切分后加载到显卡的内存中 | 存在于分布式文件系统HDFS的DataNode上,本质上是计算找数据,在存储数据切片的节点上对节点上的数据分片执行Map操作 |
| 分布式操作 | 每个GPU独立地执行前向传播计算预测值,独立地执行后向传播计算梯度并形成本地局部梯度 | TaskTracker上每个Mapper对分配的数据集独立的进行Map运算 |
| 归并操作 | 集合通讯AllReduce | TaskTracker上运行Reducer |
华为云官方文档上这张图比较完整地描述了数据并行的细节,不但覆盖了数据分配和前向传播、反向传播的过程,并且在反向传播中AllReduce的集中也包含在里面了。
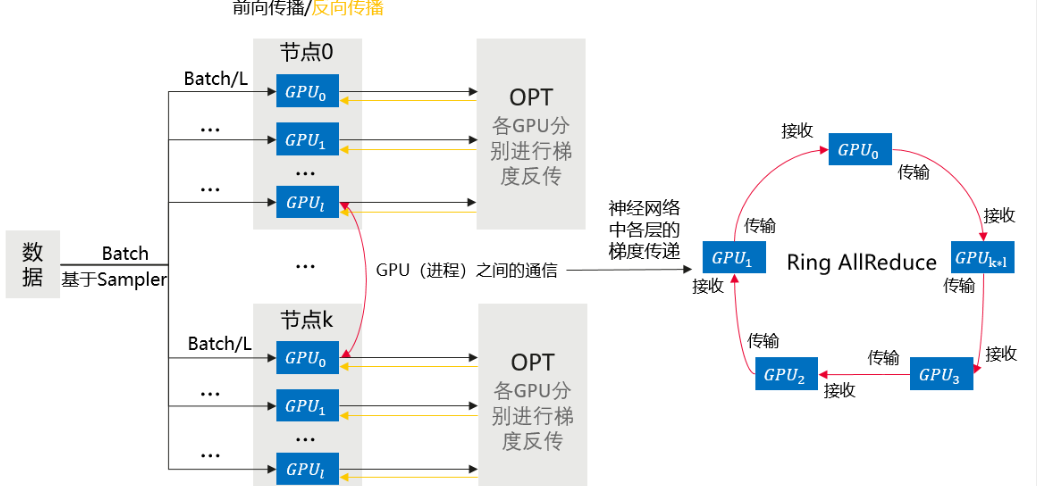
数据并行完整点流程总结大致这几个步骤:
- 在所有GPU上初始化模型的全部参数。
- 在每次训练迭代中,将随机小批量样本均匀地切分成多份,如表示为N份,分发到对应的N个GPU上。
- 每个GPU基于收到的小批量样本进行前向传播和后向传播,独立计算梯度。
- N个GPU的本地梯度聚合,得到本轮小批量样本的梯度。
- 将聚合后的梯度分发到N个GPU上。
- N个GPU根据这次小批量随机梯度,更新模型参数。
个人基于理解进一步抽象地表达了以上数据并行流程中各部分的配合关系。
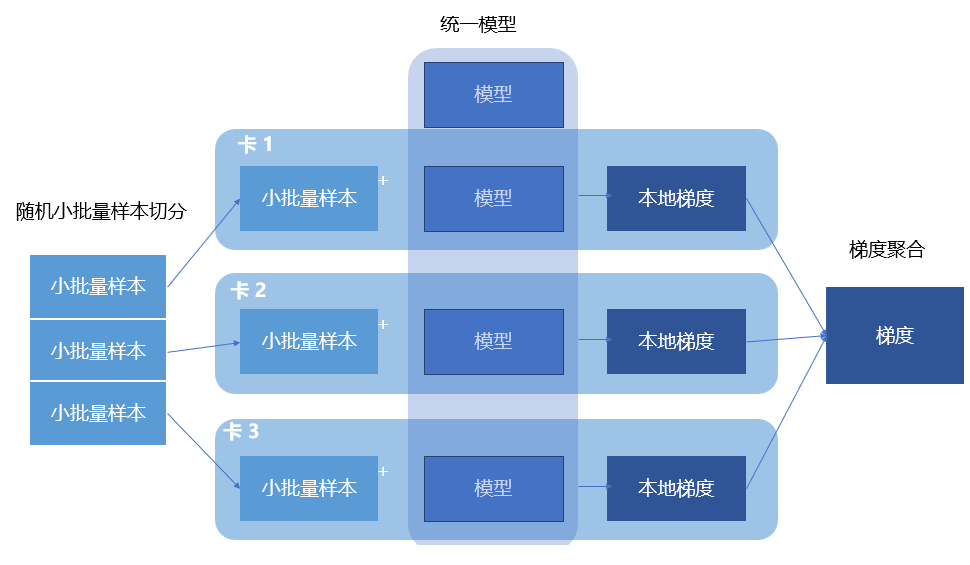
可以看到数据并行在每个GPU设备上分发完整的模型和参数,当模型比较大时很容易超过单个设备的显存容量。解决方案当然逃不出一个拆字,就是把放不下的部分进行拆分,即拆分模型,引入模型并行。有两种切法,把模型横着切,或者竖着切。对应的一种是把神经网络的不同层切分到不同的设备上,即并行发生在层间,称为流水线并行PP(Pipeline Parallelism);另一种把神经网络层内的参数切分到不同的GPU设备上,并行发生在层内,称为张量并行TP(Tensor Parallelism)。
流水线并行
流水线并行,将模型的各个层拆分到不同的GPU上并行运行。这样可以减少每个设备上的内存消耗,同时提高效率。数据在神经网络的层间移动,物理上就是在不同的GPU间移动。简单理解逻辑上就像Linux的管道操作,或者很多编程语言里链式编程:
1QueryBuilder queryBuilder = new QueryBuilder()
2 .select("Id", "name", "age")
3 .from("users")
4 .where("age > 22")
5 .orderBy("Id")
6 .limit(50);
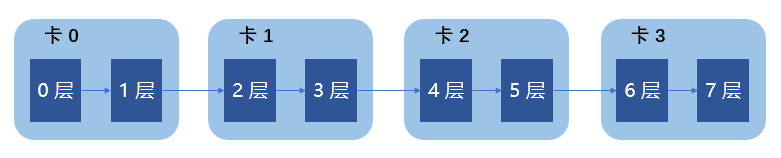
如图示意的8层神经网络,模型的不同层被分配到不同的GPU卡上。每两层规划在一个GPU设备上。当数据从0层到1层、2层到3层都是在一个卡内传播,而从1层到2层、3层到4层会垮了不同的卡设备,产生通讯开销。对于流水线并行最需要考虑好在一个阶段执行的时候另外一段流水线空等待的问题,专业上把这种空闲叫气泡Bubble。解决气泡有各种专业的设计,多数思路和典型的操作系统流水线类似,把作业划分的再细一些,把mini-batch切分成micro-batch,并行的粒度更小一些,更容易流水线并行。这只是大体思路,怎样在流水线上配合好前向计算和反向计算,考虑最大化的利于缓存有很多的设计可以做。
张量并行
张量并行将神经网络的模型、权重在GPU设备之间进行拆分。将张量沿着一定维度拆分成块,每个GPU设备上只处理一块。输入张量与权重张量相乘时,就使用矩阵乘法把权重矩阵基于列方向切分,每列分别与输入相乘,每个设备只计算权重矩阵的部分矩阵乘法,最后两个设备的分片连接起来组成最终输出。
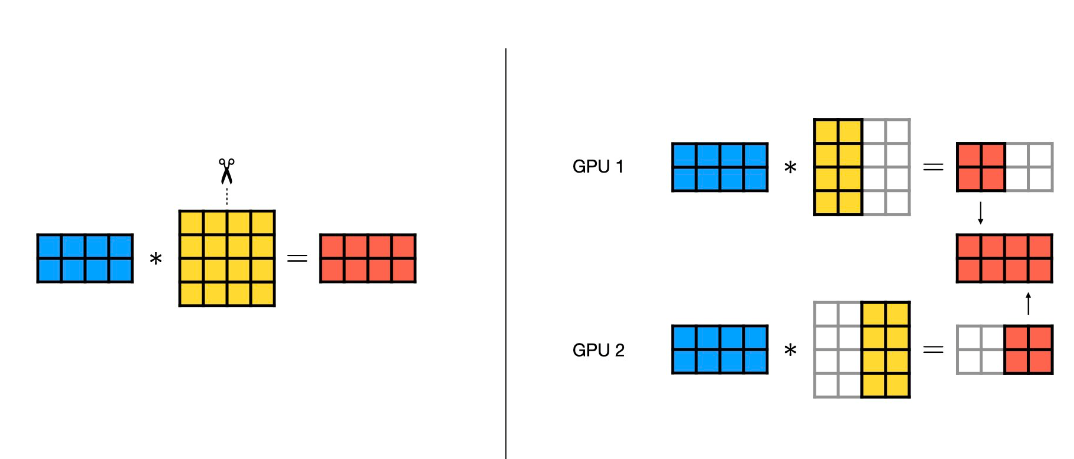
参照Pytorch 关于TP的说明,如下图。一个蓝色的2行4列的矩阵乘以一个黄色的4行4列的矩阵,会得到一个2行4列的红色矩阵。使用按列切分的张量并行,将第二个矩阵按列切分成两个4行2列的矩阵,则蓝色矩阵和两个切分的黄色矩阵的乘法可以分配到2张GPU卡上。GPU1计算矩阵乘得到一个2行2列的矩阵,GPU2计算另外一部分列的矩阵乘得到另外一个2行2列的结果。然后通过AllGather通信操作汇聚两个结果,得到一个2行4列的矩阵。和理论上不切分时矩阵乘结果一致。
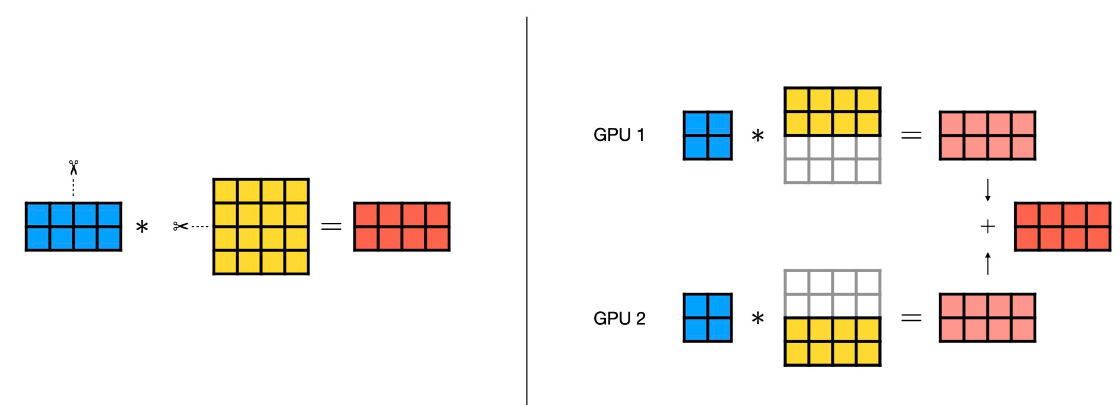
也可以基于行切分,如下图,第二个黄色矩阵按行切分进行张量并行,黄色矩阵切分成两个2行4列的矩阵。为了满足矩阵乘法要求,蓝色矩阵要配合按列切分成两个2行2列的矩阵。在两个GPU上并行执行矩阵乘,分别得到两个2行4列的矩阵。然后通过AllReduce操作将两个矩阵的结果累加得到最终的相乘结果。
更多的是行列混合切分,如Pytorch官方这个图。蓝色、黄色、绿色三个矩阵连成得到一个目标矩阵。使用张量并行,把黄色矩阵按列切分,绿色矩阵按行切分分配到两个GPU上,并行计算矩阵乘。两个GPU卡上计算结果通过AllReduce操作得到最终的相乘结果。
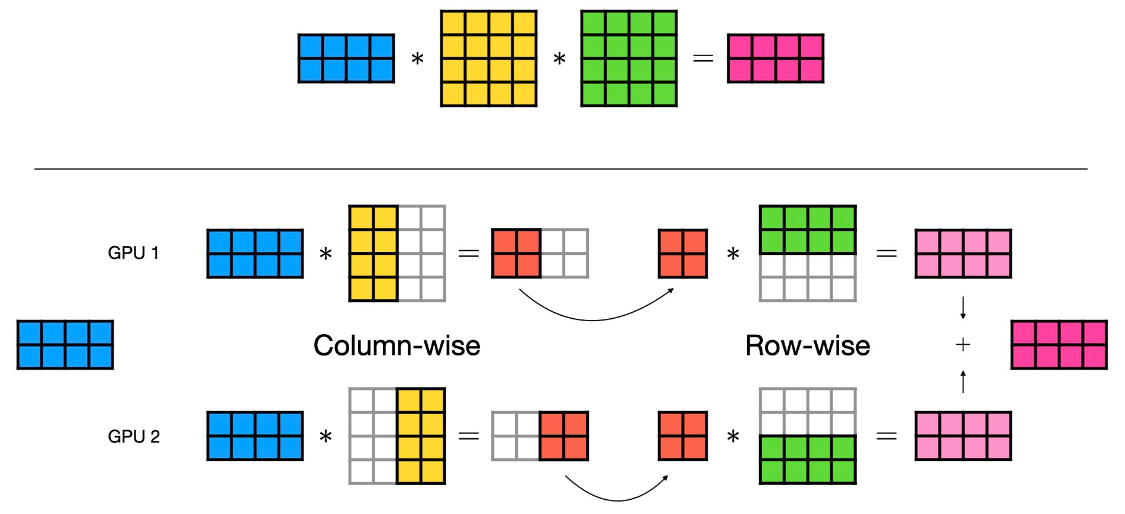
混合并行
以上,从原理上大致总结对比了下数据并行、流水线并行和张量并行。实际的模型训练中极少有只使用一种并行方式的场景,经常是几种并行一起使用,即混合并行。
开源深度学习训练优化库DeepSpeed使用混合了数据并行、张量并行、流水线并行的3D混合并行进行万亿参数的训练。结合文章《DeepSpeed: Extreme-scale model training for everyone》的几个图理解混合并行:首先从左到右划分了不同的阶段,这是流水线并行,网络的0到7层、8到15层、16到23层、24到31层分别属于一个流水线阶段;每个流水线阶段通过张量并行再划分为4块MP0、MP1、MP2、MP3;上下两个分组表示把训练数据拆分到上下两组设备Rank0、Rank1,进行数据并行。
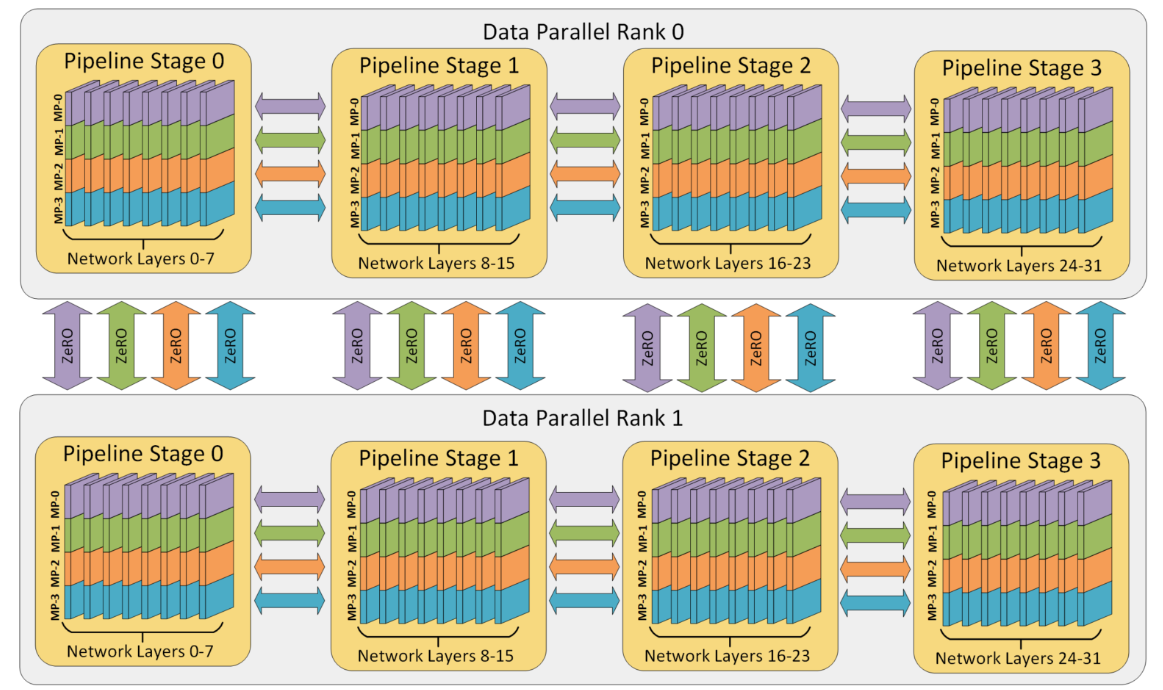
可以看到混合并行能兼顾各种并行策略的优点,最大限度地提高效率,提高性能。其中张量并行通讯开销最大,一般建议在一个节点内,或各个大厂的Scale Up超节点内,使用内部设备间的高速带宽如NVlink互联。流水线并行将模型的不同层分散到不同的机器上运算,运算结果和中间数据通过机器间的网络传递。在这个内部并行的基础上,外部进行数据并行,每组服务器处理小批量的不同数据切片,这样服务器的计算资源可以充分地被利用,提高并发量,进而提高训练速度。
同一篇文章中这张图忽略了细节更抽象地表达三种并行混合效果,相同颜色的表示在一个节点的GPU上。可以看到同一个节点的GPU间作模型并行,跨节点的GPU间作流水线并行和数据并行。
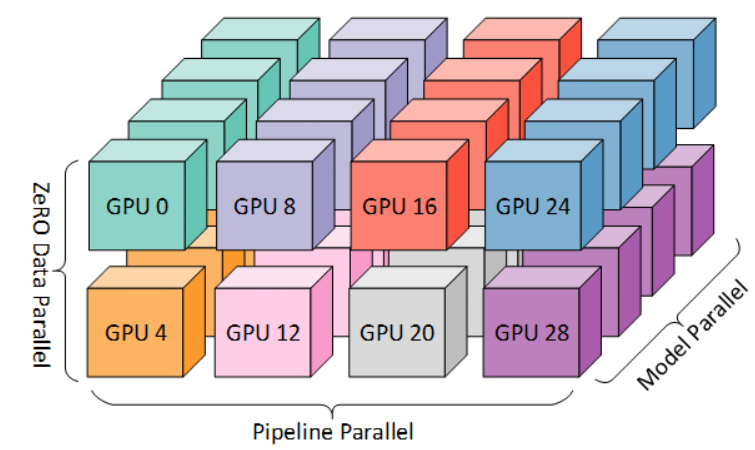
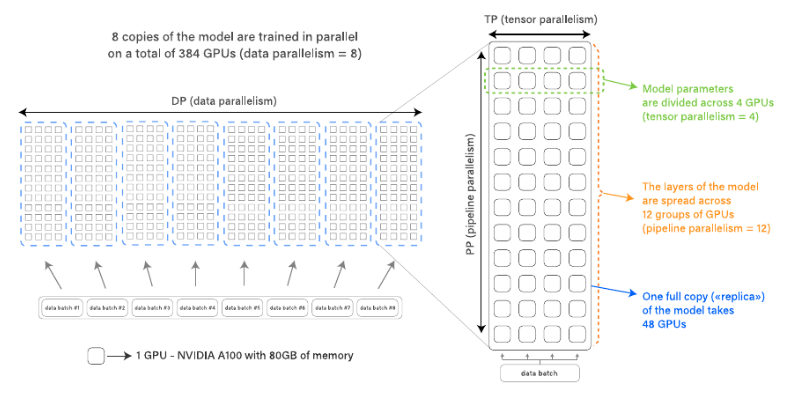
以上都是来自论文的描述,为了和实际应用结合理解,找到了一个案例:BLOOM模型训练的一个集群。由48个NVIDIA DGX-A100服务器组成,每个服务器包含8张A100 GPU,共384张卡。
从外往里看:基于最外围的数据并行,将总的训练数据分发到左边虚线框框住的8组GPU服务器上并行处理,每个框捏的48个GPU服务器处理一个模型副本,8组间的GPU服务器处理不同的数据批量分组。这样就做到了8个模型副本在384个GPU设备上进行数据并行训练的效果,通过提高并发量,提升训练速度。数据并行的并行度是8。再看每个框内,框内的每一行有4个GPU设备,模型参数划分到4个GPU设备上进行张量并行,张量并行的并行度是4。要求这4个GPU间保证告诉通讯带宽,一般这4个GPU在一个服务器内部。从图上看到框内总共有12行,或者说12层,12个层间的GPU分组间进行流水线并行。流水线并行的并行度是12。
分布式训练如此重要,所以大部分深度学习框架TensorFlow、Pytorch、MindSpore、PaddlePaddle等在神经网络开发库也都提供了分布式训练能力。如Pytorch内置了完备的张量并行,流水线并行和数据并行的处理。
框架已经提供了完备的能力,怎么在资源供给上跟的上是我们这些下层平台工程师们需要考虑的问题。虽然折腾的还是我们熟悉的计算、存储、网络。提供高质量的计算资源、节点内网络、节点间网络,将这些深度学习框架开发的训练任务按照其并行的要求调度到对应的资源节点上。这是以Kubernetes为代表的云原生技术最擅长的事情,也是我们每天都在做的事情。在Kubernetes中,当用户创建工作负载时,复杂每个实例的Pod作为基本调度单元会调度到业务期望的目标节点上,丰富的调度策略基于资源、亲和性等要求控制负载调度。在AI场景下,Kubernetes提供的这种能力达到提高资源利用率,特别是稀缺的GPU资源算力,从而已经成为面向AI资源管理的标准底座。
如根据前面不同并行策略对资源的不同要求进行拓扑亲和调度,基于最优的资源组合分配,保证模型训练性能,如优先将模型并行的任务调度到高速互联的卡上。同时,考虑到同一个训练任务基于Kubernetes调度到不同节点时,若只是部分Pod调度成功,则可能会空等待未调度成功的任务,引起资源浪费。甚至多个作业互相等待资源,可能出现资源死锁。在AI调度中引入组调度Gang Schedule实现调度过程只有满足全部资源要求是才进行调度。另外为了提高资源利用率、减少资源碎片,也有各种装箱算法优先填满一个节点或网路。在调度中也可以让离线的训练和在线的推理等任务混部。当在线任务资源低谷时,通过调度使用空闲的资源运行训练任务。当响应要求高的在线任务到来时驱逐离线任务,从而保证总体资源利用率。
除了计算的调度外,Kubernetes对存储、网络的使用都可以以一种更Native的方式扩展到AI场景。如前面描述多轮训练时,生成的数据量大无法全部在内存存储,势必引入大量的本地缓存。基于Kubernetes的存储插件对接厂商或开源的高性能分布式文件系统已经成为一个标准选择,大量应用到AI训练场景中。
毕竟大家越来越发现提高智力的唯一路径就是提高算力,大力出奇迹越来越被认可。这些通过云原生的方式进行资源管理是我们比较熟悉的。通过AI业务本身逐步深入的理解,希望能帮助我们更好地管好大模型,运维好大模型,构建一个强大的AI-Infra。
写到这里发现居然点题了。
最后
说到最后,最近才开始入坑新领域,新事物入门时,习惯用个人的文字描述出来,自说自话,基本要求比原始资料友好眼熟即可。另外一个习惯,相信事物总是通的,在跨领域或者一个大的领域范围内,不自觉地会对新东西适当抽象并和之前熟悉的领域对象进行横向对比,东拉西扯,尝试贯通。因此文中有些描述,特别是有些另类视角的比较忽略了不少细节,只是做个思路导入,就全当个托儿吧。